While computers converse in the binary tongue, humans require a more relatable language. Enter hexadecimal, the charming chameleon of computing that bridges the gap between human intuition and the machine's digital domain.

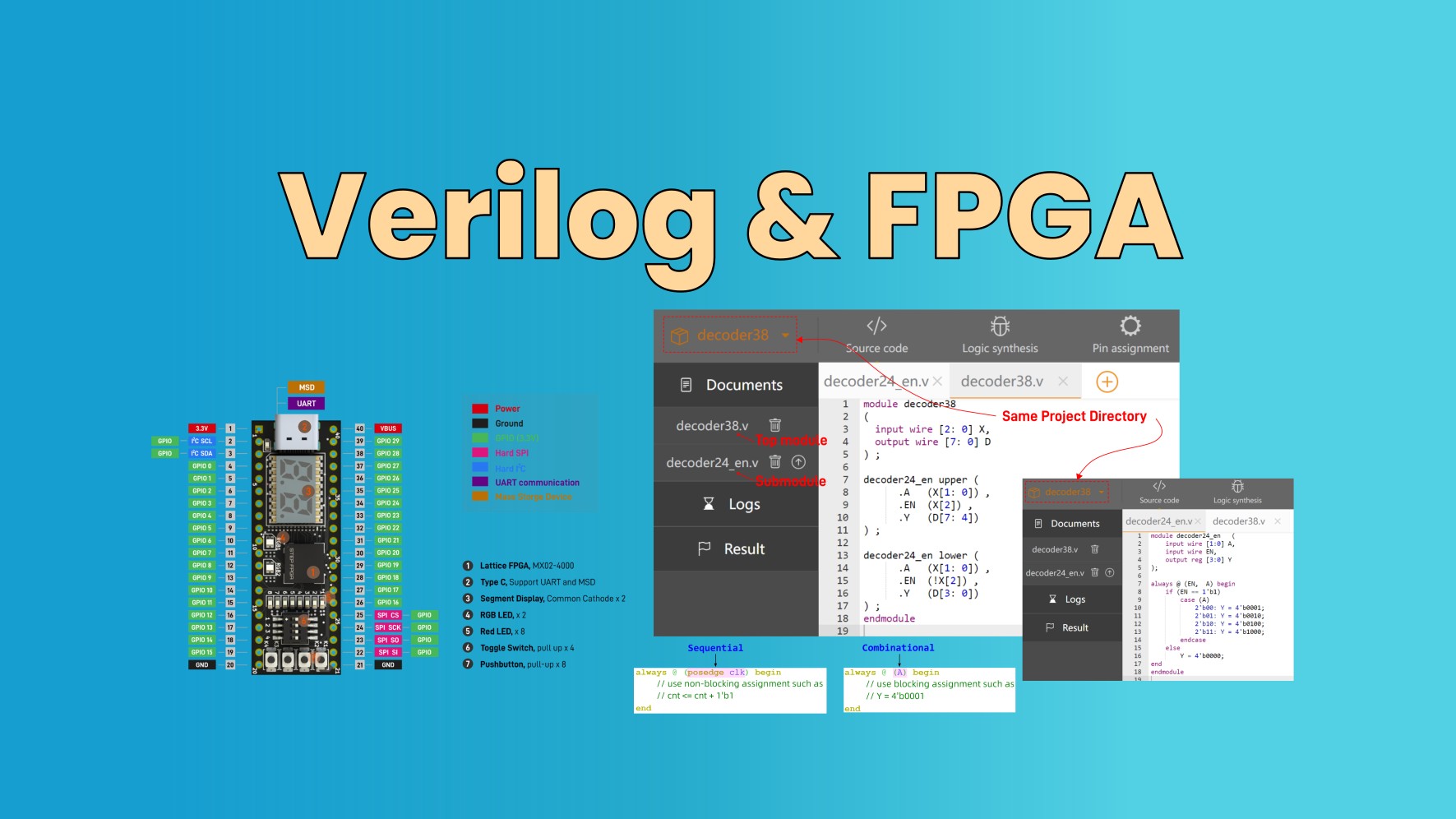
Each digit in hexadecimal represents 4 bits, making it easy to intuitively convert to binary. For example, if you have a hexadecimal number and its last digit is 9, you can immediately determine that the corresponding binary representation ends with 1001:

• Hexadecimal 9 corresponds to binary 1001.
• Hexadecimal 19 corresponds to binary 1 1001.
• Hexadecimal 119 corresponds to binary 1 0001 1001.

     

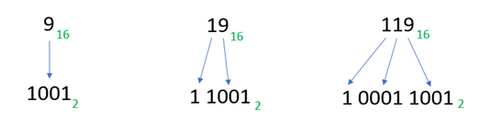
However, if you’re given a decimal number with the last digit as 9, do you know its binary equivalent? Clearly, it’s not immediately obvious.

• Decimal 9 corresponds to binary 1001.
• Decimal 19 corresponds to binary 1 0011.
• Decimal 119 corresponds to binary 111 0111.
  

In decimal, you must know all the digits in each place value to convert it to binary. This lack of intuitiveness makes converting complex decimal numbers to binary challenging.

Therefore, we can conclude that hexadecimal is a friend of binary, but decimal is not.

Why is hexadecimal a friend of binary?

The key lies in the fact that the base 16 (hexadecimal) is a power of 2 (2^4 = 16), whereas base 10 (decimal) is not. Other bases like octal (base 8, 2^3), hexadecimal (base 16, 2^4), and even higher (e.g., base 32, 64) are also friends of binary.

You might wonder why we don’t use base 32. While base 32 allows representing 5 bits with each digit, it becomes less readable for humans. In hexadecimal, familiar digits (0-9) occupy 10 positions, leaving only 6 letters (a-f) to represent the remaining values. This simplicity makes hexadecimal more manageable for humans.

Additionally, using hexadecimal has another crucial reason:

• A byte consists of 8 bits.

Memory addressing occurs at the byte level, so the chosen numbering system must effectively express a byte (8 bits).

Just a quick info: We have addressed the topic Byte vs Bit in our blog > Byte vs Bit - The relationship between a byte and a bit explained. 

While base 256 (2^8) would be ideal (one digit per byte), it’s not practical due to readability. Hexadecimal strikes a balance: one hexadecimal digit represents half a byte (4 bits), and two hexadecimal digits correspond to a full byte.

So why 8 bits per byte and not 7 or 9? The answer is historical:

• Early computers used various byte sizes (e.g., 4, 6, or 7 bits).
• However, 4 or 6 bits were too limiting for representing letters, numbers, and punctuation.
• In 1963, ASCII standardized 7-bit character encoding, but IBM System/360 mainframes adopted 8-bit bytes, leading to their widespread use. Microcomputers later followed suit.

For starting the digital electronics, check out Digital Electronics / Digital Circuits & FPGA Learning Kit with Tutorial Book

Check our other learning kits on > https://shop.eimtechnology.com/collections/diy-learning-kit

EIM technology, is developing a series of electronics learning kits for beginners and adults with an aim to provide end-to-end learning solution to the enthusiast like you.
Follows us for more blog updates.