We know the using Ohm's Law we can calculate the value of a resistor. We have discussed ohm's law in our previous blog. But, it not always easy to practically calculate the the resistor's value. The lower the resistance value, the better. In practice, many designers set the maximum voltage drop across the resistor to 100mV at the highest current as a compromise point. However, regardless of the chosen value and the associated voltage drop, the 'optimal' value of the resistor will always be debated and criticized.

Ohm's Law & Current Sensing Resistor

Is choosing a current sensing resistor easy? By simply measuring the voltage across a known resistor and then applying Ohm's Law and I=V/R (Figure 1) to determine the current, people have high expectations for this basic function. So, is there anything simpler than this?

As shown in Figure1, the principle of using resistor R and the associated voltage drop V (at point B-C) to measure the current I (from A to D) is straightforward, but there are also some subtle nuances that must be acknowledged. When the current is in the range of 100 milliohms and below, a four-wire high-impedance Kelvin detection method is typically used.

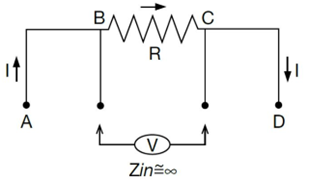
Figure 1 Measuring R in the circuit

But in reality, this is not simple either. Firstly, there is the issue of determining the resistance value. On one hand, a larger value will increase the voltage drop across its terminals, resulting in a larger reading amplitude, thereby improving the signal-to-noise ratio and resolution accuracy. However, using a larger resistance value will waste electrical energy and may potentially impact circuit stability because it adds more "idle" resistance between the power source and load, leading to increased self-heating of the resistor.

Therefore, lower resistance values are preferable. In practice, many designers set the maximum voltage drop across the resistor to 100mV at the highest current as a compromise point. However, regardless of the chosen value and the associated voltage drop, the "optimal" value of the resistor will always be subject to debate and criticism, and it also depends on the priorities of current sensing.

The Issue of IR Voltage Drop

The apparent IR voltage drop issue is the first of two closely related problems, with the second problem being the inevitable consequence of the decision made in addressing the first. Regardless of the chosen resistance value, it will generate self-heating, which is a subtle yet significant issue, especially when the current sensing resistor carries several amperes or more of current. Despite the nominal values being low (typically only milliohms), this is unavoidable: when currents in the ampere range flow, watt-level heat dissipation occurs.

Resistor Self-heating & Temperature Coefficient of Resistance (TCR)

The second imminent issue is that this self-heating will alter the nominal value of the current sensing resistor itself, thereby compromising the readings of the perceived current values. So what can be done? Unless the current is in the milliampere or microampere range, where self-heating is negligible, any responsible designer must use the Temperature Coefficient of Resistance (TCR) data provided by the supplier to analyze the resistance variation, as shown in Figure 2. Note that this analysis might even be an iterative process, as resistance variation could affect the current (depending on the reasons for the driving current entering the load), which in turn could affect self-heating, thereby influencing the resistance.

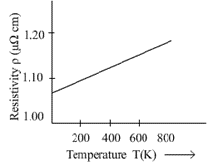
Figure 2. The function relationship between the resistivity of nickel-chromium alloy and absolute temperature

TCR is typically not a negligible small number. It is generally measured in parts per million per degree Celsius (ppm/°C); a standard 1% resistor has a TCR of around several thousand ppm/°C. The total resistance change is a function of the materials used in the resistor component, rated power, and the actual physical dimensions of the component.

Current sensing accuracy

The budgeting of overall current sensing accuracy error needs to consider three factors: initial resistance tolerance, TCR error caused by environmental temperature changes, and TCR error caused by self-heating. Fortunately, suppliers provide specialized precision metal foil resistors with extremely low TCR.

They achieve this goal by using various alloys mixed with copper, manganese, and other elements in a "secret sauce," as well as employing production techniques that manage and utilize the lowest possible TCR. For example, Bourns' CRL2010-FW-R015E is a 51mΩ, 1% device with a TCR of ±200ppm/°C. This is a tricky alloy recipe; for instance, counterintuitively, copper is often added to the mixture despite its nominal TCR being as high as 4000ppm/°C because it can improve overall heat dissipation and reduce self-heating.

To achieve ultimate precision measurements in instrument applications, resistors with the lowest TCR also come with fully characterized curves of resistance versus temperature, which take a parabolic shape and depend on the alloy combination.

Although basic TCR-related calculations may seem straightforward, any high-precision analysis must account for the fact that TCR itself is nonlinear. TCR of resistor leads must also be considered in high-precision analysis.

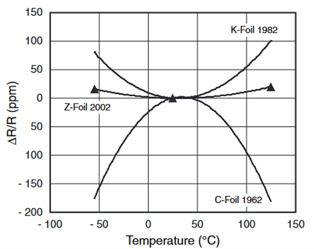
Figure3. The resistance-temperature characteristics of three different metal foil resistors (along with their introduction years) exhibit different TCR nonlinearity.

Of course, some applications do not require extremely high accuracy, and rough measurements will suffice. For these cases, standard resistors can be used. However, in many situations, it is indeed necessary to choose reasonable consistency, accuracy, and resistance self-heating. At these times, TCR can easily lead to significant errors in estimated current values.

Current sensing selection

Designers must decide whether to use lower-cost current sensing resistors, which requires accepting or managing the TCR drift effects they generate, or to use higher-cost devices with extremely low TCR. Another option is to choose resistors with higher wattage, larger physical size, moderate TCR but better dissipation characteristics, or to add a miniature heat sink to the resistor. Regardless of the chosen method, there will undoubtedly be questions during design reviews about why other methods were not selected.

Despite being "just a resistor" for the simple V=IR relationship, its impact can be significant. In systems such as electric vehicles/hybrid cars with large battery packs, photovoltaic arrays, or motor drives, using inaccurate current values may lead to unpredictable behavior, non-compliant performance and efficiency, or even safety hazards.

Have you ever encountered unexpected issues due to TCR, environmental temperature changes, or resistor self-heating in current sensing resistors? How did you address it in your design? Did you ultimately opt for non-resistor current sensing solutions?

Learn Basic Electricity/ Basic Electronic Circuits with our Electrical Circuits Learning Kit - Basic Electronics Tutorial